Single cell data modeling and local low-rank representation
With the development of biotechnology and bioinformatics, scientists deposited a series of powerful weapons in the arsenal targeting precision medicine, which also lead us toward the era that seeing through the biological process in an unprecedented resolution. Still, lack of detailed mathematic interpretation, the knowledge we retrieved from data is very limited. For instance, from scRNA-seq, each cell is characterized by its expression profile of over 20000 genes. Classic analysis methods enables us to generate several cell clusters for different cell types or physiological states from such an informative data set. However, how certain biological processes vary through cell types, how the cells interplay with each other, and what gene sets are determinant in the process, remain largely unsolved. Besides scRNA-seq, single cell FISH, single cell epigenomic and genomic data are also capable of profiling cell in high dimensional space. Another challenge is to integrate the multi-omics data on single cell level to offer more mechanism level interpretation of the cross talk among cells in a complex tissue. To further increase the resolution of our computational modeling in analyzing high-dimensional data, start from scRNA-seq with a special focus on cancer microenvironment, we proposed an LTMG model to investigate transcriptional changes or transcriptional stages of each gene from profiled cells. In this way, we rationally discretize continuous scRNAseq data with biological explainable states, such as transcriptional regulatory states or variation among cell types. Furthermore, LTMG showed robustness as have smallest KL divergence that model scRNAseq and scFISH together. Next, borrow the ideas from Non-negative Matrix Factorization (NMF) and Boolean Matrix Factorization (BMF), we developed in-house Discretized data factorization methods (UG, MG, RG) in finding coregulation modules within discretized expression data. These modules are then form our cornerstone in deciphering biological knowledge.
Software developed for this research topic include:
LTMGSCA: Left Truncated Mixture Gaussian Model based Single cell RNA-seq data Analysis
- Paper 1: https://www.biorxiv.org/content/early/2018/09/29/430009 (Nucleic Acids Research, Volume 47, Issue 18, 10 October 2019, Page e111, https://doi.org/10.1093/nar/gkz655)
- Paper 2: https://www.biorxiv.org/content/10.1101/181362v1
- GitHub link: https://github.com/zy26/LTMGSCA
M3S: A comprehensive model selection for multi-modal single-cell RNA sequencing data
- Paper is accepted by ICIBM2019 and BMC Bioinformatics (In press)
- GitHub link: https://github.com/zy26/M3S
QUBIC2: A novel biclustering algorithm for large-scale bulk RNA-sequencing and single-cell RNA-sequencing data analysis
- Paper: https://www.biorxiv.org/content/10.1101/409961v1 (Nucleic Acids Research)
- GitHub link: https://github.com/maqin2001/qubic2
BRIC: biclustering-based gene regulation inference and cell type prediction from single-cell RNA-Sequencing data
- GitHub link: https://github.com/zy26/BRIC
Complex disease microenvironment study
Computational method development
Biomedical data are often collected from bio-samples of diverse backgrounds, where each sample is characterized with high dimensional features. We are interested in extracting information from such a high dimensional and highly heterogeneous dataset, so as to discover complex inter-feature correlations that may exhibit similar behaviors on a subset of samples. This motivates us to develop methods for comprehensive detection of local low rank modules in a large matrix and/or tensor.
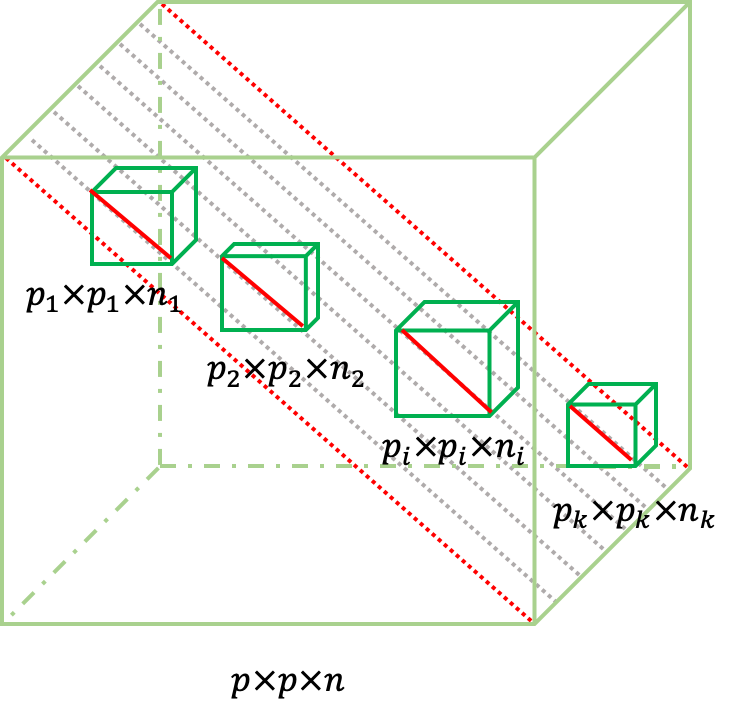
- Subspace clustering. We are inspired to find index sets {\(I_{k} \times J_{k},\ k = 1,\ldots,K\)}, where \(I_{k}\) are indices of features, and \(J_{k}\) are indices for samples, for the \(k\)th low rank module. And we aim to find such index set \(I_{k} \times J_{k}\) that satisfy the following conditions: \[\operatorname{rank}\left( X_{k} \right) \leq r,\] where \[ X_{k} = \left\{ X_{\text{ij}},(i,j^{'}) \in I_{k} \times J_{k} \right\},\] subject to \[\left| I_{k} \right| > I_{0};\left| J_{k} \right| > J_{0}.\]
- Binary matrix/tensor decomposition. Lots of complex relationships have been curated by other scientists, as well as our own efforts, and it includes cell–cell interactions, cell-gene interactions, cell-cell-gene interactions, etc. When extracting information from such relational data, we are dealing with binary matrix or tensor. To foster meaningful biological interpretation, we aim to detect modules of in the binary matrix or tensor, where a tight relational network exist. In other words, we are interested in finding low rank representation of a binary matrix/tensor, to guide a data-driven segmentation of relational networks.

- Robust mixture regression. Mixture regression models have been applied to address problems in which there exists multiple hidden groups in the population, each of which may be modeled by a different regression model in regards to covariate(s) and response variables.